Is it true that everything starts most simply?
If it is, then let us be studying the Planck Units.

Please note: This document is subject to updates.  The first draft was posted online in September 2012. There were simple updates in March 2015.

Abstract: Analyze three very simple concepts taken from a high school geometry class, (1) the smallest-and-largest measurement of a length, (2) dividing and multiplying by 2, and (3) nested-embedded-and-meshed geometries. Though initially a simple thought exercise (hardly an experiment), our students quickly developed a larger vision to create a working framework to categorize and relate everything in the known universe. Though appearing quite naïve and overly ambitious in its scope, the work initially began at the Planck Length and proceeded to the Observable Universe in somewhere over 202.34+ base-2 exponential notations. That range of notations is examined and the unique place of the first sixty notations is reviewed. This simple mathematical progression and the related geometries, apparently heretofore not examined by the larger academic community, are the praxis; interpreting the meaning of it all is the theoria, and here we posit a very simple foundation to open those discussions. Along this path it seems we will learn how numbers are the function and geometries are the form, how each is the other’s Janus face, and perhaps even how time is derivative of number and space derivative of geometry.

Simple Embedded Geometries, The Initial Framework For A Question

Observing how the simplest geometric objects are readily embedded within each other, a high school geometry class¹ asked a similar question to that asked by Zeno (circa 430 BC) centuries earlier.² “How many steps inside can we go before we can go no further?”

The students had learned about the Planck Length, a conceptual limit of 1.616199(97)x10^-35 meters. Using base-2 exponential notation, these students rather quickly discovered that it took just over 101 steps going within to get into the range of the Planck Length.

For this exercise they followed just two geometrical objects, the simple tetrahedron and the octahedron. Within that tetrahedron is an octahedron perfectly enclosed within it. Also, within each corner are four half-sized tetrahedrons.

We went inside again. At each notation or step we simply selected an object and divided the edges in half and connected those new vertices. Perfectly enclosed within the octahedron are six half-sized octahedrons in each of the six corners and eight half-sized tetrahedrons in each of the eight faces.

Selecting either a tetrahedron or octahedron, it would seem that one could divide-by-2 or multiply-by-2 each of the edges without limit. If we take the Planck Length as a given, it is not possible at the smallest scale.

And, if we take the measurements of the Sloan Digital Sky Survey (SDSS III), Baryon Oscillation Spectroscopic Survey (BOSS)³ as a given, there are also apparent limits within the large-scale universe — it is called the Observable Universe.

Also, observe how the total number of tetrahedrons and octahedrons increases at each doubling. At the next doubling there are a total of 10 octahedrons and 24 tetrahedrons. On the third doubling, there are 84 octahedrons and 176 tetrahedrons, and then on the fourth, 680 octahedrons and 1376 tetrahedrons. On the fifth step within, there are 10944 tetrahedrons and 5456 octahedrons.

The numbers become astronomically large within 101 steps. It is more aggressive than the base-2 exponential notation used with the classic wheat and chessboard story⁴ which, of course, is only 64 steps or notations.

Calculations

The following day we chased the simple math going out to the edges of the Observable Universe. There were somewhere between 101 to 105 steps (doublings or notations) to get out in the range of that exceeding large measurement, 1.03885326×10²⁶ meters. By combining these results, we had the entire “known” universe, from the smallest to the largest measurements in a range from 202.34+ notations (calculation by NASA’s Joe Kolecki) to 205.11+ notations⁵ (calculation by Jean-Pierre Luminet). At the same time, the growth of the number of objects by multiplying or dividing became such a large number, it challenged our imaginations. We had to learn to become comfortable with numbers in new ways — both exceedingly large and exceedingly small, and the huge numbers of objects.

Not long into this exploration it was realized that to achieve a consistent framework for measurements, this simple model for our universe ought to begin with the Planck Length (ℓP). It was a very straightforward project to multiply by 2 from the ℓP to the edges of the Observable Universe (OU). That model first became a rather long chart that was dubbed the Big Board – little universe⁶ And then, sometime later we began converting it to a much smaller table⁷ (Also, a working draft).

This simple construction raised questions about which we had no answers:

1. Planck Length. Why is the Planck Length the right place to start? Can it be multiplied by 2?  What happens at each step?

2. The first 65 Notations. Although we initially started with a tetrahedron with edges of one meter, in just 50 notations, dividing by 2, we were in the range of the size of a proton⁸. It would require another sixty-five steps within to get to the Planck Length. It begs the question, “What happens in each of those first 65 doublings from the Planck Length?” Could this possibly be the fabric of dark matter?

3. Embedded Geometries. When we start at the human scale to go smaller by dividing by 2, the number of tetrahedrons and octahedrons at each notation are multiplied by 4 and 1 within the tetrahedron and by 8 and 6 within the octahedron. That results in an astronomical volume of tetrahedrons and octahedrons as we approach the size of a proton. What does it mean and what can we do with that information?

Starting at the Planck Length, a possible tetrahedron can manifest at the second doubling and an octahedron could manifest at the third doubling. Thereafter, growth is exponential, base-4 and base-1 within the tetrahedron and base-8 and base-6 within the octahedron. To begin to understand what these numbers, the simple math, and the geometry could possibly mean, we turned to the history of scholarship particularly focusing on the Planck Length.

Discussions about the meaning of the Planck Length. Physics Today (Mead – Wilczek discussions).⁹ Though formulated between 1889 and 1900, the Planck Length received very little attention until C. Alden Mead in 1959 submitted a paper proposing that the Planck Length and Planck Time should “…play a more fundamental role in physics.” Though published in Physical Review in 1964, very little positive feedback was forthcoming. Frank Wilczek in that 2001 Physics Today article comments that “…C. Alden Mead’s discussion is the earliest that I am aware of.” He posited the Planck constants as real realities within experimental constructs whereby these constants became more than mathematical curiosities.

Frank Wilczek continued his analysis in several papers and books and he has personally encouraged the students and me to continue to focus on the Planck Length. We are.

The simple and the complex

A very simple logic suggests that things are always simple before they become complex. I assume I adopted this idea while growing up as a child; my father would ask, “Is there an even more simple solution?” Complex solutions make us feel smarter and wiser, yet the opposite is most often true. When teaching students from ages 12 to 18, one must always start with the simplest new concepts and build on them slowly. Then, a good teacher might challenge the students to see something new, “If you can, find a more simple solution.”

Our class was basic science and mathematics, focusing on geometry. My assignment was to introduce the students to the five platonic solids. Yet, by our third time together, we were engaging the Planck Length. Is it a single point? Is it a vertex making the simplest space? What else could it be? Can it be more than just a physical measurement? Are we looking at point-free geometry?¹⁰ Is this a pre-structure for group theory?¹¹ Speculations quickly got out of hand.

We knew we would be coming back to those questions over and over again, so we went on. We had to assume that the measurement could be multiplied by 2. We attributed that doubling to the thrust of life.¹² So, now we have two points, or two vertices, or a line, and a larger space of some kind. Prof. Dr. Freeman Dyson¹³ in a personal email suggests, “Since space has three dimensions, the number of points goes up by a factor eight, not two, when you double the scale.” We liked that idea; it would give us more breathing room. However, when we realized there would be an abundance of vertices, we decided to continue to multiply by two. We wanted to establish a simple platform using base-2 exponential notation especially because it seemed to mimic life’s cellular division, chemical bonding and bifurcation theory.

The first 60 doublings, layers, steps, or notations

Facts & Guesses. If taken-as-a-given, the Planck Length is a primary vertex and it can be multiplied by 2. The exponential progression of numbers becomes a simple fact. Guessing about the meaning of the progression is another thing. And to do so, we must hypothesize, possibly just hypostatize, the basic meanings and values. In our most far-reaching thoughts, this construct seems to open up possibilities to intuit an infrastructure or pre-structure that just might-could create a place for all that scholarship that doesn’t appear to have a grid and inherent matrix — philosophies, psychologies, thoughts and ideas throughout time. So herein we posit a simple fact and make our most speculative guesses:

• Within the first ten doublings, using simple math — multiplying by 2 — there are over 1000 vertices. Perhaps we might think about Plato’s Eidos, the Forms. Now, Prof Dr. Freeman Dyson of the Institute for Advance Studies suggests that each time we should be multiplying by 8 (not by 2). This would result in an astronomically large number of vertices.
• Within twenty doublings, there are over a million vertices. What about Aristotle’s Ousia or Categories?
• Within thirty steps, there are over a billion vertices. Perhaps we could hypostatize Substances, a fundamental layer that anticipates the table of elements or periodic table.
• Within forty layers, there are over a trillion vertices. Might we intuit Qualities?
• Within 50 doublings, there over a quadrillion vertices. How about layers for Primary Relations, the precursors of subjects and objects?
• At the 60th notation, still much smaller than the proton, there are over a quintillion vertices. Perhaps Systems and The Mind, and every possible manifestation of a mind, awaits its place within this ever-growing matrix or grid.
• The simple mathematics for these notations, virtually the entire small-scale universe, appears to be the domain of elementary cellular automata going back to the 1940s work of John von Neumann, Nicholas Metropolis and Stanislaw Ulam, and the more recent work of John Conway and his Game of Life, and the most recent work of Stephen Wolfram and his research behind A New Kind of Science.

With so many vertices, one could build a diversity of constructions, then ask the question, “What does it mean?” Our exercise with the simplest math and simple concepts is the praxis. We have begun to turn to the history of scholarship to begin to deem the theoria and begin to see if any of our intuitions might somehow fit. We knew our efforts were naïve, surely a bit idiosyncratic (as a prominent physicist had personally commented to me in email¹⁴), but we were attempting to create a path that would take us from the simplest to the most complex. If we stayed with our simple math and simple geometries, we figured that we did not have to understand the dynamics of protons, fermions, scalar constraints and modes, gravitational fields, and so so much more. That could come later.

Although not studied per se, these 60 notations have been characterized throughout the years. Within the scientific age, it has been discussed as the luminiferous aether (ether).¹⁵ Published in 1887 by Michelson–Morley, their work put this theory to rest for about a century. Yet, over the years, the theories around an aether have been often revisited. The ancient Greek philosophers called it quintessence¹⁵ and that term has been adopted by today’s theorists for a form of dark energy.

Theories abound.

Oxford physicist-philosopher, Roger Penrose¹⁶ calls it, Conformal Cyclic Cosmology made popular within his book, Cycles of Time. In a September 24, 2008 interview on NBC News (Cosmic Log), Frank Wilczek of MIT simply calls this domain, the Grid,¹⁷ and the most complete review of it is within his book, The Lightness of Being. We know with just two years of work on this so-called Big Board – little universe chart and much less time on our compact table, we will be exploring those 60-to-65 initial steps most closely for years to come. This project will be in an early-stage development for a lifetime.

From Parameters to Boundaries and Boundary Conditions

This construction with its simple nested geometries and simple calculations (multiplying the Planck Length by 2 as few as 202.34 times to as many as 205.11 times) puts the entire universe in an mathematically ordered set and a geometrically homogeneous group. Although functionally interesting, quite simple and rather novel, is it useful?

Some of the students thought it was. This author thought it was. And, a few scholars with whom we have spoken encouraged us. So the issue now is to continue to build on it until it has some real practical philosophical, mathematical, and scientific applicability. Taking our three simple parameters just as they have been given, (1) the Planck Length, (2) multiplication by 2 and (3) Plato’s simplest geometry, what more can we say about this simple construct? Let me go out on a limb here:

1. Parameters. These parameters have functions; each creates a simple order and that order creates continuity. The form is order and the function is “to create continuity or its antithesis, discontinuity.” As a side note, one could observe, that this simple parameter set is also the beginning of memory and intelligence.

2. Relations. The parameters all work together to form a simple relation. From four points, a potential tetrahedron, simple symmetries are introduced. With eight points, the third doubling, a potential simple octahedron could become manifest. All the parameters work together to provide a foundation for additional simple functions to manifest. The form is the relation and the function is “to make and break symmetries.”

3. Dynamics. Our simple parameters, now manifesting real relations that have the potential to be extended in time, create a foundation for dynamics, all dynamics. That is the form with the potential to become a category, and the function is to create various harmonies or to create disproportion, imbalance, or disagreement. Dynamics open us to explore such concepts as periodicity, waves, cycles, frequency, fluctuations, and more. And, this third parameter set, dynamics-harmony, necessarily introduces our perception of time. With this additional parameter set we begin to intuit what might give rise to the fullness of any moment in time and of time itself. Also, perspectivally, these parameter sets, on one side, just might could summarize perfection or a perfected moment in time, and on the other side, imperfection or quantum physics. Please note that our use of the double modal, might could, is a projection for future, intense analysis and interpretation. It is a common expression in the New Orleans area.

Perfections and Imperfections. The first imperfection can occur very early within the notations (doublings-steps-layers). With the first doubling there are two vertices (the smallest line or smallest-possible string). At the next doubling, there are four vertices; a perfect tetrahedron could be rendered. It is the simplest three-dimensional form defined by the fewest number of vertices and equal angles. There are other logical possibilities: (1) four vertices form a longer line or string, (2) four vertices form a jagged line or string of which various skewed triangles and polygons could be formed, (3) three vertices form a triangle that defines a plane with the fourth vertex forming an imperfect tetrahedron that opens the first three dimensions of space. Five vertices can be used to create two tetrahedrons with a common face. Six vertices could be used to create an octahedron or three abutting tetrahedrons (two faces are shared).

The third doubling renders eight vertices. With just seven of those vertices, a pentagonal cluster of five tetrahedrons can be inscribed. The earliest analysis of these five regular tetrahedra sharing one edge appears to be the work of F. C. Frank and J.S. Kaspers in their 1959 analysis of complex alloy structures. There is a gap of about 7.36° (7° 21′) or less than 1.5° between each face.¹⁹ 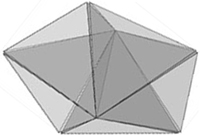There are many other configurations of a five-tetrahedral construction that can be created with those seven vertices. These will be addressed in a separate article. For our discussions here, it seems that each suggests a necessarily imperfect construction. The parts only fit together by stretching them out of their simple perfection. One might speculate that the spaces created within these imperfections could also provide room for movement or fluctuation.

With all eight vertices, a rather simple-but-complex figure can be readily constructed with six tetrahedrons, three on either side of a rather-stretched pyramid filling an empty space between each group. This figure has many different manifestations using just eight vertices. Between seven and eight vertices is a key step in this simple evolution. Both figures can morph and change in many different ways, breaking-and-making perfect constructions.

A few final flights of imagination

In one’s most speculative, intuitive moments, one “might-could” see these constructions as a way of engaging the current work with the Lie Group,²⁰ yet here may begin a different approach to continuous transformations groups. Just by replicating these eight vertices, a tetrahedral-octahedral-tetrahedral (TOT) chain emerges. Here two octahedrons and two tetrahedrons are perfectly aligned by the eight and a simple structure reaching from the smallest to the largest readily emerges and tiles the universe. Then, there is yet another very special hexagonal tiling application to be studied within the octahedron by observing how each of the four hexagonal plates interact with all congruent tetrahedrons.

Within all these notations, steps or doublings, simplicity begets complexity. Structures become diverse. And, grids of potential and a matrix of possibilities are unlocked.

Endnotes, Footnotes and References: (Work-in-progress)

¹ Monday, December 19, 2011 Bruce Camber substituted for the geometry teacher within the John Curtis High School, just up river from New Orleans. The concept of a Big Board – little universe developed within the context of these classes. That work continues today.

² We should all be as curious as Zeno. His paradoxes are widely studied even today. Zeno of Elea (ca. 490 BC – ca. 430 BC) is a pre-Socratic Greek philosopher, a member of the Eleatic School founded by Parmenides. Known for his paradoxes to understand the finite and infinite, we will be revisiting Zeno often.

³ For most students, the wheat & chessboard example is their introduction to exponential notation. Wikipedia provides an overview.

⁴ “Most Precise Measurement of Scale of the Universe,” Jennifer Ouellette, Discover Magazine, April 6, 2012

⁵ On Wednesday, July 17, 2013, Prof. Dr. Jean-Pierre Luminet wrote: “I tried to understand the discrepancy between my calculation and that of Joe Kolecki. The reason is simple. Joe took as a maximum length in the universe the so-called Hubble radius, whereas in cosmology the pertinent distance is the diameter of the observable universe (delimited by the particle horizon), now estimated to be 93 billion light years, namely 8.8 10^26 m. In my first calculation giving the result 206, I took the approximate 10^27 m, and for the Planck length 10^(-35) m instead of the exact 1.62 10^(-35) m. Thus the right calculation gives 8.8 10^26 m / 1.62 10^(-35) m = 5.5 10^(61) = 2^(205.1). Thus the number of steps is 205 instead of 206. You can quote my calculation in your website.” – Jean-Pierre Luminet, Directeur de recherches au CNRS, Laboratoire Univers et Théories (LUTH), Observatoire de Paris, 92195 Meudon Cedex http://luth.obspm.fr/~luminet/

⁶ Big Board – little universe, a five foot by one foot chart that begins with the Planck Length and uses exponential notation to go to the width of a human hair in 102 steps and to the edges of the observable universe in 202.34-to-205.11 notations, or steps, or doublings.

⁷ Universe Table, ten columns by eleven rows, this table is made to be displayed on Smartphones and every other form of a computer. At the time of this writing, Version 1.0.0.2. was posted..

⁸ Taking just the octahedron, the calculation is: 6⁶⁵=3.8004172ex10⁵⁰ octahedrons and 8⁶⁵= 5.0216814e⁵⁸ tetrahedrons. Add to that, with the tetrahedrons at each step are four tetrahedrons: 4⁶⁵=1.3611295ex10³⁹ and the additional octahedron within it at each step : 1⁶⁵=65

⁹ Frank Wilczek, the head of the Center for Theoretical Physics at MIT and a 2004 Nobel Laureate has a series of articles about the Planck Length within Physics Today. Called Scaling Mt. Planck, these are all well-worth the read. His book, The Lightness of Being, to date, is his most comprehensive summary.

¹⁰ Point-free geometry, a concept introduced by A. N. Whitehead in 1919/1920, was further refined in 1929 within his publication of the book, Process & Reality. More recent studies within mereotopology continue to extend Whitehead’s initial work. Also, the study of concepts in pregeometry in physics and model theory are helpful.

¹¹ One might speculate that group theory, with its related subjects such as combinatorics, fields, representation theory, system theory and Lie transformation groups, all apply in some way to the transformation from one notation to the next. Yet, two transformations seem to beg for special attention. One is from the Human Scale to the Small Scale and the other from the Human Scale to the Large Scale. With our range of notations from 201+ to 205 notations, our focus might turn to steps 67 to 69 at the small scale and 134 to 138 at the large scale universe. One’s speculations might could run ahead of one’s imaginative sensibilities. For example, at the transformation to the small scale, approximately in the range of the diameter of a proton, one could hypostatize that this is where the number of embedded geometries begins to contract to begin to approach the most-simple structure of the Planck Length. It would follow that within the small-scale all structures would necessarily be shared. Perhaps the proton is some kind of a boundary for individuation. That is, the closer one gets to the singularity of the Planck Length, the more those basic geometric structures within the notation are shared. Because this structure currently appears to be beyond the scope of measuring devices, we could refer to these notations as a hypostatic science, whereby hypotheses, though apparently impossible to test, are still not beyond the scope of imagination and logic. Also, as the large scale is approached, somewhere between notations 134 to 138, there might be a concrescence that opens the way to even more speculative thinking. Though not very large — between 248 miles (notation 134) and- 3500 miles (notation 138) — it might appear to be silly, truly nonsensical, to begin the search for the Einstein-Rosen bridges or wormholes! That’s certainly science fiction. Yet, if we let an idea simmer for awhile, maybe workable insights might-could begin to emerge.

¹² Although the term, Thrust of Life, is used within religious and philosophical studies, it is also the subject of continuous scientific study by groups such as the Center for Science for of Information (Purdue University) through funding from the National Science Foundation.

¹³ Personal email to me regarding multiplying the Planck Length by 2, he said: “Since space has three dimensions, the number of points goes up by a factor eight, not two, when you double the scale.” Certainly a cogent comment, however, given we have seemingly more than enough vertices, we decided on the first pass to continue to multiply by 2 to create an initial framework from which attempt to grasp what was important and functional.

¹⁴ In a personal email to me regarding the initial posting for Wikipedia, a prominent physicist said: “…it’s certainly an idiosyncratic view, not material for an encyclopedia.”

¹⁵ The luminiferous aether was posited by many of the leading scientists of the 18th century, Sir Issac Newton (Optiks) being the most luminous. The Michael-Morley experiments of 1887 put the theory on hold such that the theory of relativity and quantum theory emerged. Yet, research to understand this abiding concept has not stopped. And, it appears that the editorial groups within Wikipedia are committed to updating that research.

¹⁶ Quintessence, the Fifth Element in Plato’s Timaeus, has been used interchangeably with the aether aether. It has a long philosophical history. That the word has been adopted in today’s discussion as one of the forms of dark energy tells us how important these physicists believe dark energy is.

¹⁷ Roger Penrose inspired the 1998 book, The Geometric Universe: Science, Geometry, and the Work of Roger Penrose. Surely Penrose is one of the world’s leading thinkers in mathematics and physics. He has been in the forefront of current research and theory since 1967, however, his work on Conformal Cyclic Cosmology is not based on simple mathematics or simple geometries. It is based on the historic and ongoing tensions within his disciplines. Though his book, Cycles of Time, written for the general population, it is brings all that history and tension with it.

¹⁸ Frank Wilczek has written extensively about the Planck length. He recognizes its signature importance within physics. When we approached him with our naive questions via email in December 2012, we did not expect an answer, but, we received one. It was tight, to the point, and challenged us to be more clear. Given he was such a world-renown expert on such matters, we were overjoyed to respond. The entire dialogue will go online at some time. He is a gracious, thoughtful thinker who does not suffer fools gladly. And because we believe, like he does, in beauty and simplicity, perhaps there will be a future dialogue that will further embolden us.

¹⁹ Frank, F. C.; Kasper, J. S. (1958), “Complex alloy structures regarded as sphere packings. I. Definitions and basic principles”, Acta Crystall. 11. and Frank, F. C.; Kasper, J. S. (1959), and “Complex alloy structures regarded as sphere packings. II. Analysis and classification of representative structures”, Acta Crystall. 12. More recently, this construct has been analyzed by the following: (1) “A model metal potential exhibiting polytetrahedral clusters” by Jonathan P. K. Doye, University Chemical Laboratory, Lensfield Road, Cambridge CB2 1EW, United Kingdom, J. Chem. Phys. 119, 1136 (2003) The compete article is also available at ArXiv.org as a PDF: http://arxiv.org/pdf/cond-mat/0301374‎ (2) “Polyclusters” by the India Institute of Science in Bangalore has many helpful illustrations and explanations of crystal structure. PDF: http://met.iisc.ernet.in/~lord/webfiles/clusters/polyclusters.pdf (3) “Mysteries in Packing Regular Tetrahedra” Jeffrey C. Lagarias and Chuanming Zong, a focused look at the history.

²⁰ The work of Sophus Lie (1842 – 1899), a Norwegian mathematician, not only opened the way to the theory of continuous transformation groups for all of mathematics, it has given us a pivot point within group theory by which to move our analysis from parameters to boundary conditions and on to transformations between each notation. We are hoping that we are diligent enough to become Sophus Lie scholars.

___________________________________________________________________

About the author

In 1970 Bruce Camber began his initial studies of the 1935 Einstein-Podolsky-Rosen (EPR) thought experiment. In 1972 he was recruited by the Boston University School of Theology based on (1) his research of perfected states in space-time through work within a think tank in Cambridge, Massachusetts, (2) his work within the Boston University Department of Physics, Boston Colloquium for the Philosophy of Science, and (3) his work with Arthur Loeb (Harvard) and the Philomorphs. With introductions by Victor Weisskopf (MIT) and Lew Kowarski (BU), he went to CERN on two occasions, primarily to discuss the EPR paradox with John Bell. In 1979, he coordinated a project at MIT with the World Council of Churches to explore shared first principles between the major academic disciplines represented by 77 peer-selected, leading-living scholars. In 1980 he spent a semester with Olivier Costa de Beauregard and Jean-Pierre Vigier at the Institut Henri Poincaré focusing on the EPR tests of Alain Aspect at the Orsay-based Institut d’Optique. In 1994, following the death of another mentor, David Bohm, Camber re-engaged simple interior geometries based on several discussions with Bohm and his book, Fragmentation & Wholeness. In 1997 he had made  molds made to produce thousands of the tetrahedron and octahedron. These are used in the models throughout these discussions. In 2002, he spent a day with John Conway at Princeton to discuss the simplicity of the interior parts of the tetrahedron and octahedron. In 2011, he challenged a high school geometry class to use base-2 exponential notation to follow the interior structure of basic geometries from the Planck Length and to the edges of the Observable Universe.

****
Afterthought: Could cellular automaton apply to the first 65 doublings from the Planck Length using base-2 exponential notation to PRE-STRUCTURE things?

More than things, as in protons and fermions, could the results of cellular automaton be understood as Plato’s Forms or Eidos (perhaps notations 2-to-10) and Aristotle’s Ousia (perhaps doublings 10-to-20)? Assuming the Planck Length to be a vertex, and assigning the area over to pure geometries, do we have the basis for form, structure, and the architecture for substances? Then, could it be that this architecture gives rise to an architecture for qualities (notations 20-to-30)? And, as we progress in the evolution of complexity, could it be that in this emergence, there is now an architecture for relations (notations 40-to-50)? If we assume an architecture for relations, could the next be an architecture for Systems (notations 50-to-60) and this actually becomes the domain of the Mind? It is certainly a different kind of ontology given it all begins with cellular automaton and base-2 notation provide a coherent architecture (with built in imperfections of the five-tetrahedral cluster also known as a pentastar).