| Small Scale Speculations Ideas |
Concepts and Parameters |
Boundaries |
Trans- |
Numbers and Number Theory |
Forms, Order, Relation and Dynamics | Functions Continuity, Symmetry, Harmony |
Large Scale |
||
| 1 Planck Length ( ℓP ) |
Transition: Small-to-Human Scale |
1. Display area: Every number/word hyperlinked – quick results display here 2. Options: Open full screen, new tab or window to the research of the experts 3. Also: Related videos-images and online collaborations with up to nine visitors 4. Key Links: http://bblu.org Universe-View.org BigBoardLittleUniverse.org |
Transition: Human-to-Large Scale |
205+ Observable Universe |
|||||
| 2- 10 Forms1 Vertices:1024 |
77 Research ℓP:2.44×10-12m |
78 X-ray Wavelength |
95 Range: Visible Light |
96 Bacteria Red Light |
113 Hand-sizeH 16.78+cm |
114 TextbookT 12.8+inches |
131 Marathon 27+miles |
132 54+ miles 87.99+km |
204+ Observable Universe |
| 11-20 Structure-Ousia V: 1+million |
76 Gamma Wavelength |
79 Huang Scale |
94 Nanoparticles 100-10000+nm |
97 Blood cellR 2.4+microns(µm) |
112 Finger-size 3.3″(inches) |
115 Things 67.134±cm |
130 Race 21.998+km |
133 Drive 108+miles |
202-203+ Observable Universe |
| 21-30 Substances V:1+ billion |
75 Falstad Scale |
80 Periodic Table |
93 Gold LeafG 160.06±nm |
98 Capillary 5.12+microns |
111 Spoonful 4.19+cm |
116 A child 52.86±in |
129 Distances: 6.834+miles |
134 Gravity-free 351.97+km |
198-201 Superclusters 6.1-54+yottometers |
| 31-40 Qualities V:1+ trillion |
74 Research 1.52+x10-13m |
81 HydrogenH 31±pm |
92 Nanowires 80.03±nm |
99 Cells 10.24±microns |
110 MakeupM .82±inches |
117 A bed 105.72±inches |
128 Village 3.41±miles |
135 Distance 437.41±miles |
191-197 Virgo Supercluster3 |
| 41-50 Relations V:1+ quadrillion |
73 Research: Tunneling4 |
82 HydrogenH 78+ pm |
91 Little chipslc 40.01+nm |
100 Sperm 20.48+microns |
109 LipstickL 1.04+centimeters |
118 Bedroom 5.37+meters |
127 Walk 1.7+miles |
136 Fly 874+miles |
181-190 Galactic Group6 |
| 51-60 Systems The MindM |
72 NucleusN 7.63+x10-14m |
83 CarbonC 70±pm2 |
90 Viruses 20.007+nm |
101 HAIR 40+microns |
108 DiamondD 5.2+mmM |
119 Home 35.24+feet |
126 Downtown 1.37+km |
137 Rivers 2815.81+km |
171-180 Milky Way |
| 61-65 Elementary Particles |
71 GoldAU Nucleus |
84 WATERW 3.12+x10-10m |
89 Cell Wall 10+nm |
102 Paper 81.95+microns |
107 Ants 2.62+mm |
120 Property 21.48+m |
125 Superdome 687.45+m |
138 USA-to-UK 3500+miles |
161-170 SolarS Interstellar |
| 65-67 Neutron Proton-Fermion |
70 AluminumAl 1.90+x10-14m |
85 DNAD 6.25+x10-10m |
88 Insulin 5.00+x10-9m |
103 EggE .16+millimeters |
106 Sand 1.31+mm |
121 Yacht 142+feet |
124 Skyscraper 343.7+meter+ |
139 EarthE 11,263+km |
151-160 Solar SystemS |
| 68 HeliumHe 4.77+x10-15 m |
69 Electron 9.54+x10-15m |
86 Buckyballs 1.25+nm |
87 Ribosomes 2.50+nm |
104 >.< Period .32+mm |
105 Bacterium .65+mm |
122 Sequoia 85+meters |
123 Tall Building 171.86+m |
140 GPS Satellite 22526+km |
141-150 Earth Systems |
Category: Education
Freeman Dyson: A Guiding Light
![]() From: Freeman Dyson
From: Freeman Dyson
Date: Mon, Oct 22, 2012 at 11:12 AM
Subject: Re: 34 years later… Might it be useful to see the universe as 202.34 notations that are necessarily related through simple geometries all nested within each other?
To: Bruce Camber
Dear Bruce Camber,
Thank you for the invitation to comment. Without seeing your scheme, it is hard to judge whether it would make sense. If I take your three questions literally, the answer is No to all three.
1. Since space has three dimensions, the number of points goes up by a factor eight,* not two, when you double the scale.
2. The universe we live in is not nested at all. On the contrary, larger levels of structure are quite different from smaller levels. Larger levels bring qualitatively new structures. For example, a galaxy does not look like a big star, and a star does not look like a big planet, and a planet does not look like a big elephant, and an elephant does not look like a big bacterium, and a bacterium does not look like a big atom.
3. I don’t know any recent work that would be important for your project. There are plenty of new pictures for you to choose from, both in the large and in the small, from galaxies to viruses.
Sorry I do not have any more useful ideas. I will be interested to see what comes out of your project.
Yours sincerely,
Freeman Dyson
* Editor’s note and reference: http://www.av8n.com/physics/scaling.htm We can extend this idea into three dimensions. The volume goes up by a factor of eight because the cube is twice as wide…
Here is the letter to which Prof. Dr. Freeman Dyson was responding:
On Fri, 19 Oct 2012, Bruce Camber wrote:
> Dear Prof. Dr. Dyson:
> Just over 34 years ago I contacted you regarding a special project at MIT called,
> “An architecture for integrative systems.” It was a display project in the main rotunda
> just off Massachusetts Avenue. It borrowed Erwin Schrodinger’s title from his much
> earlier work, a book entitled, “What is life?” Seventy-seven leading, living scholars
> participated and you were one of them. We are taking that old product and re-purposing
> it online within a very similar framework — Small Scale, Human Scale, Large Scale —
> however, we are using base-2 exponential notation from the Planck Length to the
> edges of the observable universe which gives us 202.34 ordered steps in which to context
> information. By assuming nested geometries at each doubling, it seems that we
> will have an inherent structure for analogous or metaphorical connection-making.
>
> But before we go too far, I would like to re-engage you and ask for your advice:
> 1. If the Planck Length is a dimensionful number representing a singularity
> or a point, can we multiply it by 2 and assume two points? …multiply it again
> and assume 4, then 8, 16, 32 and on up to 1024 by the 10th doubling?
> 2. Can we assume nested geometries throughout?
> 3. We will use the same infrastructure as used by Wikipedia to build it out, so
> owner’s of information can readily edit and update content. Is there any particular
> recent work to which you would want us to take note?
>
> Thank you.
>
> Warmly,
>
> Bruce
Just what are we to believe about anything?
Last update: Sunday, September 7, 2014
Please note: This page was first posted within the Small Business School website (television series about best business practices). Bruce Camber and his wife, Hattie Bryant, were the creator/founders. A few links just may still go back to Small Business School. You can use your back button to come back to this article.
__________
Constants1 and universals2 are inherent throughout all of life. Most often based on a combination of logic, mathematics, and consistent measurements, these concepts appear to be true throughout all time and within any space (certainly within defined parameters and boundary conditions). Some people believe these concepts can actually open pathways to understand how it is that there is space and time, and human life and consciousness. It is all so bewildering and the sciences and mathematics around these issues so complex and seemingly impenetrable, people everywhere yearn for compelling but somewhat easier answers to these big questions about the meaning and value of life.
Many religions3 are not very religious and are best understood as a cult.4 Some philosophies also qualify. Simply stated, cults are the people and their organized set of beliefs that are primarily based on their founding documents, historic writings lifted up as the highest principles and concepts around which one can orient their life. Though it might seem that many types of organizations could be labelled a cult, it is far from the truth. Although basic beliefs within any organization come from their writings, balanced organizations give as much, if not more weight and importance to their best scholars’ research, writings and teachings about their historical statements and how these work with the constants understood throughout the sciences and universals understood by the most-respected scholars throughout time. Most cults offer more simplified answers to such questions. And for their followers, these answers become their Absolute5 framework, the fundamentals of their belief system.
That definition of a cult is also the beginning of a working definition of fundamentalism.6 It does not matter what the belief system is; fundamentalists are mostly caught up with the fundamentals that have been defined within a particular space at a particular time. As already observed, these are historic moments. The scientific community is not exempt. It has its own group of fundamentalists among their secularists. These folks stridently proclaim that Atheism is the only true “religion” or system of belief about ultimate things. The radical atheists take what has been given by the sciences, and boldly proclaim, “We have the only right answers. This is the Way, the Truth, and the Light.”
Mainstream religions and philosophies context their belief system within our known understanding of universals & constants. Although the focused study of the universals-and-constants is mostly the domain of natural sciences, other disciplines — logic, mathematics and ethics — also open this world. Our best scientists know that their natural sciences are still young and there are many new worlds and universes yet to explore.
Both types of fundamentalists — religious and scientific — fall short.
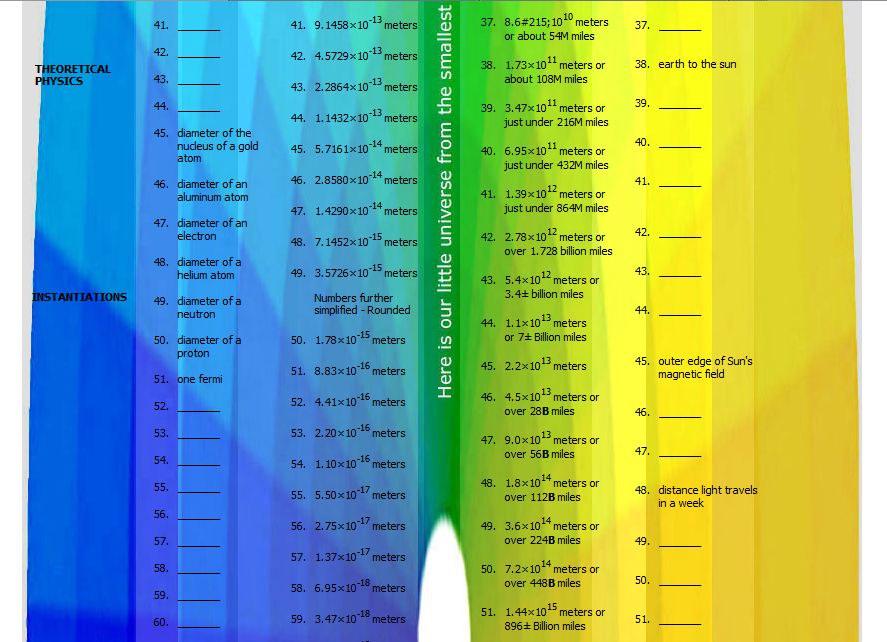
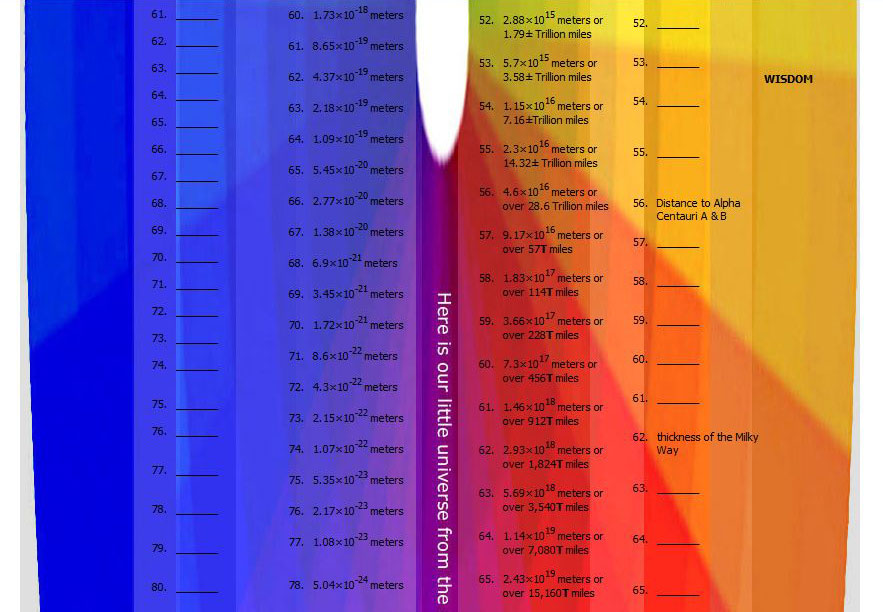
There are profoundly simple constants-universals that have not been fully explored and are not generally recognized by the world’s scientific community that could begin to change things. A very simple example was the focus of five high school geometry classes that asked, “How many steps would it take to get to the Planck length using base-2 exponential notation assuming nested geometries all the way?” We found about 101 steps going within to the Planck length going all just by dividing each edge within each step by 2 (and connecting those new vertices) and about 101 steps to the Observable Universe going out by multiplying by 2.
We put it all on a board with a full-spectrum color wheel as the background and called it the Big Board-little universe (BB-lu).
It appears to be the first time people would see the entire universe from the smallest to the largest, all mathematically notated and necessarily related, on one long board in somewhere over 201 steps or doublings. Perhaps this simple scale based on the Planck length could open new worlds to explore at CERN’s Large Hadron Collider. To the best of our current knowledge, steps 1 to 60 have never been discussed as such.
So, this discussion is not a science versus faith discussion. It is a focus on the ways we approach and interpret both science and religion. It is about exegesis and hermeneutics. Most often those two studies are only about the way we interpret religious texts, particularly sacred scripture; however, both can also be applied to the sciences, especially regarding the limitations of science and the edge of discovery.
How and why do teachers become fundamentalists? Where do they go wrong?
Let us start with a focus on Radical Islam and scientific Atheism. We gave this question some attention within our work with our Small Business School television series that aired on PBS-TV and the Voice of America-TV. We were asking about the root causes of 9/11. Here is a link to those studies as well as a letter to the Iran’s Grand Ayatollah Ali Khamanei back in 2006. Lumping them with the growing stridency of the today’s breed of Atheists — they, too, are demanding recognition and real power — all types of fundamentalism really need to be studied, compared and contrasted for their use or lack of use of universals and constants. Notwithstanding, because Radical Islam and her teachers demand that we acknowledge them (or they will rather arbitrarily blow us up, and they continue to threaten to kill us), we should begin with these two. Surely both are having the penultimate temper tantrum (intolerance to disagreement) so, from here let us compile studies of the most influential among their current groups of teachers.
A primary challenge for each of us is to define what is universal and constant within our own life. It is no easy task. The summary in the concluding paragraph of this article is a work-in-progress and the initial work is linked here.7 In 1979 that work included many leading , living scholars. It had begun to evolve from a study of physics and the sciences, to include religion, logic, ethics, value, and even business.8
A key question to ask is, “What concepts are shared by all of these disciplines?” Assuming you get a few answers, ask yourself, “What concepts are the most simple?” And also, “What concepts could have a face of perfection?” Those three questions opened the way to this paper’s simple working formula:
The form – the function (a face of perfection) and the imperfect quantum world
Embedded within this little formulation and the statements just above it are links to the first applications of these universals. It goes back to work in 1979 at MIT regarding first principles with 77 leading, living scholars from around the world. It has stimulated many simple explorations that seem to have been overlooked by the academics, most certainly the religionists and the fundamentalists.
A simple summary might go something like this:
Continuity defines order. Symmetries and asymmetries in some manner define all relations. The perfection of a relation is a symmetry. And, a harmony defines a perfection of multiple symmetries within a dynamic moment.
One can use religious language, metaphorical language, or scientific language to describe each. And if done well, that language is an observation of one of the faces of the same thing and each language helps to inform the other. When teachers give too much weight to one language over the other, they begin to lose their balance and fall into the trap of thinking that they just may be smarter than all the others.
—————
Over time such conclusions hurt their ability to think-and-reason. Thank you.
1 An evolving analysis of physical constants within Wikipedia (opens in a new window).
2 An evolving analysis of universals, the problem of universals as well as universal properties in Wikipedia (new window opens).
3 An evolving analysis of nature of religion can be found within Wikipedia (opens in a new window).
4 An evolving analysis of nature of cults, also within Wikipedia (opens in a new window).
5 An evolving analysis of the concepts around The Ultimate, here known as The Absolute, within Wikipedia (new window).
6 An evolving analysis of the word, fundamentalism, within Wikipedia (new window).
7 Continuity equations define most constants and beg the question, “What is continuity?” and Wikipedia has something to say.
8 Wikipedia’s references to symmetries are helpful. However, our challenge is to find the best living scholars to engage. Here Roger Penrose and Lisa Randall offer insights.
Could The Planck Length Be The Next Big Thing? Could Planck Time Be A Gateway To The Universe?
Is it true that everything starts most simply?
If it is, then let us be studying the Planck Units.
Please note: First draft posted online in September 2012. Simple updates in March 2015. Timeline for the author (also posted within his business, Small Business School).
Abstract: Analysis of three very simple concepts taken from a high school geometry class are: (1) the smallest-and-largest measurement of a length, (2) dividing and multiplying by 2, and (3) nested-embedded-and-meshed (combinatorial) geometries. Though initially a simple thought exercise (hardly an experiment), our students quickly developed a larger vision to create a working framework to categorize and relate everything in the known universe. Though appearing quite naïve and overly ambitious in its scope, the work initially began at the Planck Length and proceeded to the Observable Universe in somewhere over 202.34+ base-2 exponential notations. That range of notations is examined and the unique place of the first sixty notations is reviewed. This simple mathematical progression and the related geometries, apparently heretofore not examined by the larger academic community, are the praxis; interpreting the meaning of it all is the theoria, and here we posit a very simple foundation to open those discussions. Along this path it seems we will learn how numbers are the function and geometries are the form, how each is the other’s Janus face, and perhaps even how time is derivative of number and space derivative of geometry.
The Initial Framework For A Question
Observing how some of the simplest geometric objects are readily embedded within each other, a high school geometry class1 asked a similar question to that asked centuries earlier by Zeno (circa 430 BC).2 “How many steps inside can we go before we can go no further?”
The students had learned about the Planck Length, a conceptual limit of 1.616199(97)x10-35 meters. Using base-2 exponential notation, these students rather quickly discovered that it took just over 110 steps going within to get into the range of the Planck Length.
For this exercise they followed just two geometrical objects, the simple tetrahedron and the octahedron. Within that tetrahedron is an octahedron perfectly enclosed within it. Also, within each corner are four half-sized tetrahedrons.
 We went inside again. At each notation or step we simply selected an object and divided the edges in half and connected those new vertices. Perfectly enclosed within the octahedron are six half-sized octahedrons in each of the six corners and eight half-sized tetrahedrons in each of the eight faces.
We went inside again. At each notation or step we simply selected an object and divided the edges in half and connected those new vertices. Perfectly enclosed within the octahedron are six half-sized octahedrons in each of the six corners and eight half-sized tetrahedrons in each of the eight faces.
Selecting either a tetrahedron or octahedron, it would seem that one could divide-by-2 or multiply-by-2 each of the edges without limit. If we take the Planck Length as a given, it is not possible at the smallest scale.
 Also, observe how the total number of tetrahedrons and octahedrons increases at each doubling. At the next doubling there are a total of 10 octahedrons and 24 tetrahedrons. On the third doubling, there are 84 octahedrons and 176 tetrahedrons, and then on the fourth, 680 octahedrons and 1376 tetrahedrons. On the fifth step within, there are 10944 tetrahedrons and 5456 octahedrons.
Also, observe how the total number of tetrahedrons and octahedrons increases at each doubling. At the next doubling there are a total of 10 octahedrons and 24 tetrahedrons. On the third doubling, there are 84 octahedrons and 176 tetrahedrons, and then on the fourth, 680 octahedrons and 1376 tetrahedrons. On the fifth step within, there are 10944 tetrahedrons and 5456 octahedrons.
The numbers become astronomically large within 101 steps. It is more aggressive than the base-2 exponential notation used with the classic wheat and chessboard story4 which, of course, is only 64 steps or notations.
The following day we chased the simple math going out to the edges of the Observable Universe. There were somewhere between 101 to 105 steps (doublings or notations) to get out in the range of that exceeding large measurement, 1.03885326×1026 meters. By combining these results, we had the entire “known” universe, from the smallest to the largest measurements in a range. Initially the range began with 202.34+ notations (calculation by NASA’s Joe Kolecki), then 205.11+ notations5 (calculation by Jean-Pierre Luminet). At the same time, the growth of the number of objects by multiplying or dividing became such a large number, it challenged our imaginations. We had to learn to become comfortable with numbers in new ways — both exceedingly large and exceedingly small, and the huge numbers of objects.
Not long into this exploration it was realized that to achieve a consistent framework for measurements, this simple model for our universe ought to begin with the Planck Length (ℓP). It was a very straightforward project to multiply by 2 from the ℓP to the edges of the Observable Universe (OU). That model first became a rather long chart that was dubbed the Big Board – little universe.6 And then, sometime later we began converting it to a much smaller table7 (also, a working draft).
This simple construction raised questions about which we had no answers:
- Planck Length. Why is the Planck Length the right place to start? Can it be multiplied by 2? What happens at each step?
- The first 65 Notations. Although we initially started with a tetrahedron with edges of one meter, in just 50 notations, dividing by 2, we were in the range of the size of a proton8. It would require about sixty-five additional steps within to get to the Planck Length. It begs the question, “What happens in each of those first 65 doublings from the Planck Length?”
- Embedded Geometries. When we start at the human scale to go smaller by dividing by 2, the number of tetrahedrons and octahedrons at each notation are multiplied by 4 and 1 within the tetrahedron and by 8 and 6 within the octahedron. That results in an astronomical volume of tetrahedrons and octahedrons as we approach the size of a proton. What does it mean and what can we do with that information?
Starting at the Planck Length, a possible tetrahedron can manifest at the second doubling and an octahedron could manifest at the third doubling. Thereafter, growth is exponential, base-4 and base-1 within the tetrahedron and base-8 and base-6 within the octahedron. To begin to understand what these numbers, the simple math, and the geometry could possibly mean, we turned to the history of scholarship particularly focusing on the Planck Length.
Discussions about the meaning of the Planck Length. Physics Today (Mead – Wilczek discussions).9 Though formulated between 1889 and 1900, the Planck Length received very little attention until C. Alden Mead in 1959 submitted a paper proposing that the Planck Length and Planck Time should “…play a more fundamental role in physics.” Though published in Physical Review in 1964, very little positive feedback was forthcoming. Frank Wilczek in that 2001 Physics Today article comments that “…C. Alden Mead’s discussion is the earliest that I am aware of.” He posited the Planck constants as real realities within experimental constructs whereby these constants became more than mathematical curiosities.
Frank Wilczek continued his analysis in several papers and books and he has personally encouraged the students and me to continue to focus on the Planck Length. We are.
The simple and the complex
A very simple logic suggests that things are always simple before they become complex. I assume I adopted this idea while growing up as a child; my father would ask, “Is there an even more simple solution?” Complex solutions make us feel smarter and wiser, yet the opposite is most often true. When teaching students from ages 12 to 18, one must always start with the simplest new concepts and build on them slowly. Then, a good teacher might challenge the students to see something new, “If you can, find a more simple solution.”
Our class was basic science and mathematics, focusing on geometry. My assignment was to introduce the students to the five platonic solids. Yet, by our third time together, we were engaging the Planck Length. Is it a single point? Is it a vertex making the simplest space? What else could it be? Can it be more than just a physical measurement? Are we looking at point-free geometry? Is this a pre-structure for group theory? Speculations quickly got out of hand.
We knew we would be coming back to those questions over and over again, so we went on. We had to assume that the measurement could be multiplied by 2. We attributed that doubling to the thrust of life.12 So, now we have two points, or two vertices, or a line, and a larger space of some kind. Prof. Dr. Freeman Dyson13 in a personal email suggests, “Since space has three dimensions, the number of points goes up by a factor eight, not two, when you double the scale.” We liked that idea; it would give us more breathing room. However, when we realized there would be an abundance of vertices, we decided to continue to multiply by two. We wanted to establish a simple platform using base-2 exponential notation especially because it seemed to mimic life’s cellular division and chemical bonding.
The first 60 doublings, layers, steps, or notations
Facts & Guesses. If taken-as-a-given, the Planck Length is a primary vertex and it can be multiplied by 2. The exponential progression of numbers becomes a simple fact. Guessing about the meaning of the progression is another thing. And to do so, we must hypothesize, possibly just hypostatize, the basic meanings and values. In our most far-reaching thoughts, this construct seems to open up possibilities to intuit an infrastructure or pre-structure that just might-could create a place for all that scholarship that doesn’t appear to have a grid and inherent matrix — philosophies, psychologies, thoughts and ideas throughout time. So herein we posit a simple fact and make our most speculative guesses:
- Within the first ten doublings, using simple math — multiplying by 2 — there are over 1000 vertices. Perhaps we might think about Plato’s Eidos, the Forms. Now, Prof Dr. Freeman Dyson of the Institute for Advanced Studies suggests that each time we should be multiplying by 8 (not by 2) because of scaling laws and dimensional analysis.
- Within twenty doublings, there are over a million vertices. What about Aristotle’s Ousia or Categories? If scaling laws are applied, there would be over two quintillion vertices by the 20th notation.
- Within thirty steps, there are over a billion vertices. Perhaps we could hypostatize Substances, a fundamental layer that anticipates the table of elements or periodic table.
- Within forty layers, there are over a trillion vertices. Might we intuit Qualities?
- Within 50 doublings, there over a quadrillion vertices. How about layers for Primary Relations, the precursors of subjects and objects?
- At the 60th notation, still much smaller than the proton, there are over a quintillion vertices. Perhaps Systems and The Mind, and every possible manifestation of a mind, awaits its place within this ever-growing matrix or grid.
- The simple mathematics for these notations, virtually the entire small-scale universe, appears to be the domain of elementary cellular automata going back to the 1940s work of John von Neumann, Nicholas Metropolis and Stanislaw Ulam, and the more recent work of John Conway and his Game of Life, and the most recent work of Stephen Wolfram and his research behind A New Kind of Science.
With so many vertices, one could build a diversity of constructions, then ask the question, “What does it mean?” Our exercise with the simplest math and simple concepts is the praxis. We have begun to turn to the history of scholarship to begin to deem the theoria and begin to see if any of our intuitions might somehow fit. We knew our efforts were naïve, surely a bit idiosyncratic (as a prominent physicist had personally commented to me in email14), but we were attempting to create a path that would take us from the simplest to the most complex. If we stayed with our simple math and simple geometries, we figured that we did not have to understand the dynamics of protons, fermions, scalar constraints and modes, gravitational fields, and so so much more. That could come later.
Although not studied per se, these 60 notations have been characterized throughout the years. Within the scientific age, it has been discussed as the luminiferous aether (ether).15 Published in 1887 by Michelson–Morley, their work put this theory to rest for about a century. Yet, over the years, the theories around an aether have been often revisited. The ancient Greek philosophers called it quintessence15 and that term has been adopted by today’s theorists for a form of dark energy.
Oxford physicist-philosopher, Roger Penrose16 calls it, Conformal Cyclic Cosmology made popular within his book, Cycles of Time. In a September 24, 2008 interview on NBC News (Cosmic Log), Frank Wilczek of MIT simply calls this domain, the Grid,17 and the most complete review of it is within his book, The Lightness of Being. We know with just two years of work on this so-called Big Board – little universe chart and much less time on our compact table, we will be exploring those 60-to-65 initial steps most closely for years to come. This project will be in an early-stage development for a lifetime.
From Parameters to Boundaries and Boundary Conditions
This construction with its simple nested geometries and simple calculations (multiplying the Planck Length by 2 as few as 202.34 times to as many as 205.11 times) puts the entire universe in an mathematically ordered set and a geometrically homogeneous group. Although functionally interesting, quite simple and rather novel, is it useful?
Some of the students thought it was. This author thought it was. And, a few scholars with whom we have spoken encouraged us. So the issue now is to continue to build on it until it has some real practical philosophical, mathematical, and scientific applicability. Taking our three simple parameters just as they have been given, (1) the Planck Length, (2) multiplication by 2 and (3) Plato’s simplest geometry, what more can we say about this simple construct? Let me go out on a limb here:
1. Parameters. These parameters have functions; each creates a simple order and that order creates continuity. The form is order and the function is “to create continuity or its antithesis, discontinuity.” As a side note, one could observe, that this simple parameter set is also the beginning of memory and intelligence.
2. Relations. The parameters all work together to form a simple relation. From four points, a potential tetrahedron, simple symmetries are introduced. With eight points, the third doubling, a potential simple octahedron could become manifest. All the parameters work together to provide a foundation for additional simple functions to manifest. The form is the relation and the function is “to make and break symmetries.”
3. Dynamics. Our simple parameters, now manifesting real relations that have the potential to be extended in time, create a foundation for dynamics, all dynamics. That is the form with the potential to become a category, and the function is to create various harmonies or to create disproportion, imbalance, or disagreement. Dynamics open us to explore such concepts as periodicity, waves, cycles, frequency, fluctuations, and more. And, this third parameter set, dynamics-harmony, necessarily introduces our perception of time. With this additional parameter set we begin to intuit what might give rise to the fullness of any moment in time and of time itself. Also, perspectivally, these parameter sets, on one side, just might could summarize perfection or a perfected moment in time, and on the other side, imperfection or quantum physics. Please note that our use of the double modal, might could, is a projection for future, intense analysis and interpretation. It is a common expression in the New Orleans area.
Perfections and Imperfections. The first imperfection can occur very early within the notations (doublings-steps-layers). With the first doubling there are two vertices (the smallest line or smallest-possible string). At the next doubling, there are four vertices; a perfect tetrahedron could be rendered. It is the simplest three-dimensional form defined by the fewest number of vertices and equal angles. There are other logical possibilities: (1) four vertices form a longer line or string, (2) four vertices form a jagged line or string of which various skewed triangles and polygons could be formed, (3) three vertices form a triangle that defines a plane with the fourth vertex forming an imperfect tetrahedron that opens the first three dimensions of space. Five vertices can be used to create two tetrahedrons with a common face. Six vertices could be used to create an octahedron or three abutting tetrahedrons (two faces are shared).
The third doubling renders eight vertices. With just seven of those vertices, a pentagonal cluster of five tetrahedrons can be inscribed. The earliest analysis of these five regular tetrahedra sharing one edge appears to be the work of F. C. Frank and J.S. Kaspers in their 1959 analysis of complex alloy structures. There is a gap of about 7.36° (7° 21′) or less than 1.5° between each face.19  There are many other configurations of a five-tetrahedral construction that can be created with those seven vertices. These will be addressed in a separate article. For our discussions here, it seems that each suggests a necessarily imperfect construction. The parts only fit together by stretching them out of their simple perfection. One might speculate that the spaces created within these imperfections could also provide room for movement or fluctuation.
There are many other configurations of a five-tetrahedral construction that can be created with those seven vertices. These will be addressed in a separate article. For our discussions here, it seems that each suggests a necessarily imperfect construction. The parts only fit together by stretching them out of their simple perfection. One might speculate that the spaces created within these imperfections could also provide room for movement or fluctuation.
With all eight vertices, a rather simple-but-complex figure can be readily constructed with six tetrahedrons, three on either side of a rather-stretched pyramid filling an empty space between each group. This figure has many different manifestations using just eight vertices. Between seven and eight vertices is a key step in this simple evolution. Both figures can morph and change in many different ways, breaking-and-making perfect constructions.
A few final flights of imagination
In one’s most speculative, intuitive moments, one “might-could” see these constructions as a way of engaging the current work with the Lie Group,20 yet here may begin a different approach to continuous transformations groups. Just by replicating these eight vertices, a tetrahedral-octahedral-tetrahedral (TOT) chain emerges. Here two octahedrons and two tetrahedrons are perfectly aligned by the eight and a simple structure reaching from the smallest to the largest readily emerges and tiles the universe. Then, there is yet another very special hexagonal tiling application to be studied within the octahedron by observing how each of the four hexagonal plates interact with all congruent tetrahedrons.
Within all these notations, steps or doublings, simplicity begets complexity. Structures become diverse. And, grids of potential and a matrix of possibilities are unlocked.
Endnotes, Footnotes and References: (Work-in-progress)
1 Monday, December 19, 2011 Bruce Camber substituted for a high school geometry teacher within the Curtis School, just up river from New Orleans. The concept of a Big Board – little universe developed within the context of these classes. That work continues today.
2 We should all be as curious as Zeno. His paradoxes are widely studied even today. Zeno of Elea (ca. 490 BC – ca. 430 BC) is a pre-Socratic Greek philosopher, a member of the Eleatic School founded by Parmenides. Known for his paradoxes to understand the finite and infinite, we will be revisiting Zeno often.
3 “Most Precise Measurement of Scale of the Universe,” Jennifer Ouellette, Discover Magazine, April 6, 2012
4 For most students, the wheat & chessboard example is their introduction to exponential notation. Wikipedia provides an overview.
5 On Wednesday, July 17, 2013, Prof. Dr. Jean-Pierre Luminet wrote: “I tried to understand the discrepancy between my calculation and that of Joe Kolecki. The reason is simple. Joe took as a maximum length in the universe the so-called Hubble radius, whereas in cosmology the pertinent distance is the diameter of the observable universe (delimited by the particle horizon), now estimated to be 93 billion light years, namely 8.8 10^26 m. In my first calculation giving the result 206, I took the approximate 10^27 m, and for the Planck length 10^(-35) m instead of the exact 1.62 10^(-35) m. Thus the right calculation gives 8.8 10^26 m / 1.62 10^(-35) m = 5.5 10^(61) = 2^(205.1). Thus the number of steps is 205 instead of 206. You can quote my calculation in your website.” – Jean-Pierre Luminet, Directeur de recherches au CNRS, Laboratoire Univers et Théories (LUTH), Observatoire de Paris, 92195 Meudon Cedex http://luth.obspm.fr/~luminet/
8 Taking just the octahedron, the calculation is: 665=3.8004172ex1050 octahedrons and 865= 5.0216814e58 tetrahedrons. Add to that, with the tetrahedrons at each step are four tetrahedrons: 465=1.3611295ex1039 and the additional octahedron within it at each step : 165=65
9 Frank Wilczek, at that time, the head of the Center for Theoretical Physics at MIT and a 2004 Nobel Laureate, has a series of articles about the Planck Length within Physics Today. Called Scaling Mt. Planck, these are all well-worth the read. His book, The Lightness of Being, to date, is his most comprehensive summary.
10 Point-free geometry, a concept introduced by A. N. Whitehead in 1919/1920, was further refined in 1929 within his publication of the book, Process & Reality. More recent studies within mereotopology continue to extend Whitehead’s initial work. Also, the study of concepts in pregeometry in physics and model theory are helpful.
11 One might speculate that group theory, with its related subjects such as combinatorics, fields, representation theory, system theory and Lie transformation groups, all apply in some way to the transformation from one notation to the next. Yet, two transformations seem to beg for special attention. One is from the Human Scale to the Small Scale and the other from the Human Scale to the Large Scale. With our range of notations from 201+ to 205 notations, our focus might turn to steps 67 to 69 at the small scale and 134 to 138 at the large scale universe. One’s speculations might could run ahead of one’s imaginative sensibilities. For example, at the transformation to the small scale, approximately in the range of the diameter of a proton, one could hypostatize that this is where the number of embedded geometries begins to contract to begin to approach the most-simple structure of the Planck Length. It would follow that within the small-scale all structures would necessarily be shared. Perhaps the proton is some kind of a boundary for individuation. That is, the closer one gets to the singularity of the Planck Length, the more those basic geometric structures within the notation are shared. Because this structure currently appears to be beyond the scope of measuring devices, we could refer to these notations as a hypostatic science, whereby hypotheses, though apparently impossible to test, are still not beyond the scope of imagination and logic. Also, as the large scale is approached, somewhere between notations 134 to 138, there might be a concrescence that opens the way to even more speculative thinking. Though not very large — between 248 miles (notation 134) and- 3500 miles (notation 138) — it might appear to be silly, truly nonsensical, to begin the search for the Einstein-Rosen bridges or wormholes! That’s certainly science fiction. Yet, if we let an idea simmer for awhile, maybe workable insights might-could begin to emerge.
12 Although the term, Thrust of Life, is used within religious and philosophical studies, it is also the subject of continuous scientific study by groups such as the Center for Science for of Information (Purdue University) through funding from the National Science Foundation.
13 Personal email to me regarding multiplying the Planck Length by 2, he said: “Since space has three dimensions, the number of points goes up by a factor eight, not two, when you double the scale.” Certainly a cogent comment, however, given we have seemingly more than enough vertices, we decided on the first pass to continue to multiply by 2 to create an initial framework from which attempt to grasp what was important and functional.
14 In a personal email to me regarding the initial posting for Wikipedia (opens in new tab or window), a prominent physicist said: “…it’s certainly an idiosyncratic view, not material for an encyclopedia.”
15 The luminiferous aether was posited by many of the leading scientists of the 18th century, Sir Issac Newton (Optiks) being the most luminous. The Michael-Morley experiments of 1887 put the theory on hold such that the theory of relativity and quantum theory emerged. Yet, research to understand this abiding concept has not stopped. And, it appears that the editorial groups within Wikipedia are committed to updating that research.
16 Quintessence, the Fifth Element in Plato’s Timaeus, has been used interchangeably with the aether (ether). It has a long philosophical history. That the word has been adopted in today’s discussion as one of the forms of dark energy tells us how important these physicists believe dark energy is.
17 Roger Penrose inspired the 1998 book, The Geometric Universe: Science, Geometry, and the Work of Roger Penrose. Surely Penrose is one of the world’s leading thinkers in mathematics and physics. He has been in the forefront of current research and theory since 1967, however, his work on Conformal Cyclic Cosmology is not based on simple mathematics or simple geometries. It is based on the historic and ongoing tensions within his disciplines. Though his book, Cycles of Time, written for the general public, it is brings all that history and tension with it.
18 Frank Wilczek has written extensively about the Planck length. He recognizes its signature importance within physics. When we approached him with our naive questions via email in December 2012, we did not expect an answer, but, we received one. It was tight, to the point, and challenged us to be more clear. Given he was such a world-renown expert on such matters, we were overjoyed to respond. The entire dialogue will go online at some time. He is a gracious, thoughtful thinker who does not suffer fools gladly. And because we believe, like he does, in beauty and simplicity, perhaps there will be a future dialogue that will further embolden us.
19 Frank, F. C.; Kasper, J. S. (1958), “Complex alloy structures regarded as sphere packings. I. Definitions and basic principles”, Acta Crystall. 11. and Frank, F. C.; Kasper, J. S. (1959), and “Complex alloy structures regarded as sphere packings. II. Analysis and classification of representative structures”, Acta Crystall. 12. More recently, this construct has been analyzed by the following: (1) “A model metal potential exhibiting polytetrahedral clusters” by Jonathan P. K. Doye, University Chemical Laboratory, Lensfield Road, Cambridge CB2 1EW, United Kingdom, J. Chem. Phys. 119, 1136 (2003) The compete article is also available at ArXiv.org as a PDF: http://arxiv.org/pdf/cond-mat/0301374 (2) “Polyclusters” by the India Institute of Science in Bangalore has many helpful illustrations and explanations of crystal structure. PDF: http://met.iisc.ernet.in/~lord/webfiles/clusters/polyclusters.pdf (3) “Mysteries in Packing Regular Tetrahedra” Jeffrey C. Lagarias and Chuanming Zong, a focused look at the history.
20 The work of Sophus Lie (1842 – 1899), a Norwegian mathematician, not only opened the way to the theory of continuous transformation groups for all of mathematics, it has given us a pivot point within group theory by which to move our analysis from parameters to boundary conditions and on to transformations between each notation. We are hoping that we are diligent enough to become Sophus Lie scholars.
About the author
In 1970 Bruce Camber began his initial studies of the 1935 Einstein-Podolsky-Rosen (EPR) thought experiment. In 1972 he was recruited by the Boston University School of Theology based on (1) his research of perfected states in space-time through work within a think tank in Cambridge, Massachusetts, (2) his work within the Boston University Department of Physics, Boston Colloquium for the Philosophy of Science, and (3) his work with Arthur Loeb (Harvard) and the Philomorphs. With introductions by Victor Weisskopf (MIT) and Lew Kowarski (BU), he went to CERN on two occasions, primarily to discuss the EPR paradox with John Bell. In 1979, he coordinated a project at MIT with the World Council of Churches to explore shared first principles between the major academic disciplines represented by 77 peer-selected, leading-living scholars. In 1980 he spent a semester with Olivier Costa de Beauregard and Jean-Pierre Vigier at the Institut Henri Poincaré focusing on the EPR tests of Alain Aspect at the Orsay-based Institut d’Optique. In 1994, following the death of another mentor, David Bohm, Camber re-engaged simple interior geometries based on several discussions with Bohm and his book, Fragmentation & Wholeness. In 1997 he made the molds to create the plastic tetrahedrons and octahedrons used in the images above. In 2002, he spent a day with John Conway at Princeton to discuss the simplicity of the interior parts of the tetrahedron and octahedron. In 2011, he challenged a high school geometry class to use base-2 exponential notation to follow the interior structure of basic geometries from the Planck Length and to the edges of the Observable Universe.
*****************************************
Afterthought: Could cellular automaton apply to the first 65 doublings from the Planck Length using base-2 exponential notation to PRE-STRUCTURE things?
More than things, as in protons and fermions, could the results of cellular automaton be understood as Plato’s Forms or Eidos (perhaps notations 2-to-10) and Aristotle’s Ousia (perhaps doublings 10-to-20)? Assuming the Planck Length to be a vertex, and assigning the area over to pure geometries, do we have the basis for form, structure, and the architecture for substances? Then, could it be that this architecture gives rise to an architecture for qualities (notations 20-to-30)? And, as we progress in the evolution of complexity, could it be that in this emergence, there is now an architecture for relations (notations 40-to-50)? If we assume an architecture for relations, could the next be an architecture for Systems (notations 50-to-60) and this actually becomes the domain of the Mind? It is certainly a different kind of ontology given it all begins with cellular automaton and base-2 notation provide a coherent architecture (with built in imperfections of the five-tetrahedral cluster also known as a pentastar).
__________________________________
NASA scientist’s report regarding his calculations
Some Thoughts about Measurement
Back in December 2011, Bruce Camber and five high-school geometry classes in New Orleans involved themselves in an interesting little thought journey. When I was contacted by them, they were deeply into the process to discover that the number 2202.34 represents the ratio between the Hubble radius of the observable universe (according to the results in March 2012) and the Planck length (a number from modern quantum physics).
Here is how they did it:
1. The Hubble radius [astronomical measurement] is taken to be 1.31 x 1026 m and the Planck length [calculated] is 1.62 x 10-35 m. The Hubble radius comes from a recent estimate of the age of the universe published in Discover Magazine. The Planck length L may be calculated from: L = (hG/(2πc3))1/2 where h is Planck’s constant, G is Newton’s gravitational constant, and c is the speed of light, all in appropriate units of measure.
2. The ratio between the two distances is then found to be: 1.31 x 1026 m / 1.62 x 10-35 m = 202.34
This calculation arises from a related classroom activity, begun by Mr. Camber with those five geometry classes. The ratio is shown as a power of 2 (it could as well have been shown as a power of 10, or of any other number) in answer to the original class question, “How many times does one have to double the smallest known distance (the Planck length) to acquire the largest known distance (the present-day Hubble radius of the universe). I was consulted by Mr. Camber and assisted and advised him and his classes to produce the result shown above.
The significance of this result is that it displays the most extreme distance ratio imaginable in terms of a surprisingly finite number (202.34) of doublings. In a sense, it takes two quantities, neither of which can be adequately pictured in the mind, and shows them in ratio as a number that can be more easily pictured. I thought the exercise interesting and worth the effort and was happy to be called upon to contribute.
3. One additional note, the standard meter (1m) when compared to the Planck length corresponds to a ratio of 2115.57. We note that 2115 corresponds to 0.67m, and 2116 corresponds to 1.35m. In other words, the standard meter is not an even power-of-2 multiple of the Planck length. Mr. Camber and his classes have therefore suggested that a possible redefinition of the standard meter might be made by choosing one of these possibilities (i.e., 2115 or 2116 times the Planck length) and used to replace the present-day standard. The present day standard is based on the wavelength of a particular atomic emission line. This new standard would be based on a purely theoretical concept.
Bravo to Mr. Camber and his classes for some very nice (and out-of-the-box) original thinking!!!
– Joe Kolecki, NASA scientist, retired
An exploration of 101 steps from the smallest measurement, the Planck length, to the human scale, and then 101 more steps out to somewhere near the edge of the observable universe.
Editor’s Note: The very first posting in January 2012 about our work within geometry and base-2 exponential notation (doublings) was within our Small Business School website by Bruce Camber and Hattie Bryant. That site had been live on the web since December 1994.
Here is the very first time we would see the entire universe in just over 201+ steps, all necessarily-related notations.
 So, a warm welcome to you… this page provides access to a work-in-progress. Friends and family were the first to be invited to begin a critical review. Now, friends of friends are also being invited! The hope is that the project will be validated in its scope and logic. If the logic and scope are invalidated, the results of that process will be fully reported and analyzed. Is the Planck length the right place to start? Can a dimensionful number be multiplied by 2? What are the constants? Why are universals universal? To open these questions to discussion, more high school students will be invited to think about this model as a relatively simple way to organize information. College students, graduate students, doctoral candidates, and post-docs will be invited to consider how base-2 exponential notation — praxis — can become the basis for theoria. Everyone is invited to consider if and how these concepts might be integrated within their own.
So, a warm welcome to you… this page provides access to a work-in-progress. Friends and family were the first to be invited to begin a critical review. Now, friends of friends are also being invited! The hope is that the project will be validated in its scope and logic. If the logic and scope are invalidated, the results of that process will be fully reported and analyzed. Is the Planck length the right place to start? Can a dimensionful number be multiplied by 2? What are the constants? Why are universals universal? To open these questions to discussion, more high school students will be invited to think about this model as a relatively simple way to organize information. College students, graduate students, doctoral candidates, and post-docs will be invited to consider how base-2 exponential notation — praxis — can become the basis for theoria. Everyone is invited to consider if and how these concepts might be integrated within their own.
Here are links to key working pages for the big board.
• Our first Big Board and today’s Big Board-little universe Chart
• Today’s overview of some of the key ideas
• First article about the unfolding of the key ideas
• An article posted-then rejected by Wikipedia editors
Summary description of this page: An introduction to collaborative research of an indexed model of the universe using base-2 exponential notation. Because we start at the Planck Length and go to the Oobservable Universe, these notations are called Planck Notations (PN).
The small-scale universe: PN1 to PN67
The human-scale universe: PN67 to PN135
The large-scale universe: PN135 to PN202+
The back story: This project began within a high school geometry class in the metro New Orleans area.
Could this little model be the most simple, internally-consistent view of the universe?
| Please note: Linked references usually open in a new window and go to Wikipedia. |
| Quick Answer: Yes. The entire Universe and everything within it is mathematically notated and necessarily interrelated, all within somewhere over 201 doublings from the smallest measurement of space and time, the Planck Length and the Planck Time respectively, to the largest, the Observable Universe and the Age of the Universe, respectively. |
 Key Question: Have you seen an exquisitely detailed view of the entire universe all on a single chart? In just over 201 steps (or sets, notations, layers, groups, clusters or doublings), it goes from the smallest measurements (the base Planck Units) to their currently-known largest values. It all started in a high school geometry class so it is relatively straight forward and easy to understand, yet it opens some mystery as well. It is difficult to figure out how to interpret and work with the first 65 steps. These are extremely small and, to date, have not been addressed as such by the academic community. Yet, these steps may open a way to understand our universe and ourselves in new ways. Key Question: Have you seen an exquisitely detailed view of the entire universe all on a single chart? In just over 201 steps (or sets, notations, layers, groups, clusters or doublings), it goes from the smallest measurements (the base Planck Units) to their currently-known largest values. It all started in a high school geometry class so it is relatively straight forward and easy to understand, yet it opens some mystery as well. It is difficult to figure out how to interpret and work with the first 65 steps. These are extremely small and, to date, have not been addressed as such by the academic community. Yet, these steps may open a way to understand our universe and ourselves in new ways.
Let’s take a look (Pictured on the right, you can open it here within a new window). At the very top of the chart there are two rows of the most basic three-dimensional figures. The top five are named after Plato and are simply referred to as the five Platonic solids. It seems curious that only a very select group of people ever look inside these figures. If children did, this simple view of our universe would be second nature. Take any of those figures and divide each edge in half and connect those vertices (opens in new window). Each little circle is a vertex. Keep doing it. In just 101 steps, you will be approaching what most scientists believe is the smallest possible measurement in this universe (the Planck Length). A contemporary of Einstein, Max Planck formulated that measurement in 1899 and 1900. His most basic measurements have been around for awhile and today are generally considered to be among the fundamental constants of our universe. To make things a little easier we should start at the bottom of the left three columns of the chart at the Planck Length, 1.616199(97)x10-35 meters. Others use the simple figure, 1.616×10-35 meters or 1.616×10-33 centimeters. The next step, multiplying each result by 2, is called base-2 exponential notation. Now let’s move up the chart. At step 101 at the top of those columns on the left, we emerge with the width of a fine human hair. Multiply that by two and you are at the width of a typical piece of paper; that is step 102 on the right. Now go down those three columns on the right side of the chart. Continue to multiply by two. In just over 101 steps you will have gone out past the Sun, then exited the Solar System and then the Milky Way, and quickly pushed out to be in the range of the edges of the observable universe. We wanted to give this chart a highly-descriptive name so we called it, Big Board – little universe. Big Board – little universe: From the Planck Length to the Edges of the Observable Universe. Yes, this project started back in December 2011 in River Ridge, Louisiana just a few miles up river from New Orleans (NOLA) and just downriver from the NOLA airport. Within a few hundred feet of the river is the John Curtis Christian School. Though well-known for football, their academics are very good. In the geometry classes they had been studying the platonic solids. Strange things can happen when one is invited to be a substitute teacher, essentially just an assistant for the students and their teacher, Steve Curtis, who is part of our extended family. December 19, 2011 was the last day before the Christmas break. What a day to be a substitute! One quickly asks, “How do you keep their attention? What could catch their imagination?” For example, “How could one make that simple dodecahedron (pictured) a bit more interesting?”
The first and only other time with these students was used for model building so they could begin to explore the inside structures of the basic five. The dodecahedron was not part of that effort, so to make it more simple, we asked, “Why not make each face of that dodecahedron out of five tetrahedrons (pictured)?” That makes the familiar strange. Instead of a simple dodecahedron, this one had 60 external faces!
It was a straightforward task to do the simple base-2 math to create the first draft of what would become a rather big board. On December 17, the first draft was printed at Office Max in Harahan, Louisiana. Their widest paper for this kind of thing was 24 inches. “Let’s do it.” The resulting chart measured ten feet long. It didn’t take long to agree that it was too big and awkward so on the next day, two smaller charts, 12″ by 60″ were printed. We put the two small charts on the left and right side of the class and then cut that ten-foot board in half and put the top section in the front and the bottom in the back. The setting was magical. Now, there is a huge history of work that has already been done using base-10 exponential notation. Kees Boeke, a high school teacher, started that work in 1957 in Holland and it has become a staple of the classroom to study orders of magnitude. Although the big board is quite analogous to Boeke’s work, it has a very different sense of itself. Instead of multiplying and dividing by simply adding or subtracting a zero (0), we begin with exacting measurements given to us from Max Planck. Second, we have all of our geometries with us. So, our chart is much more visceral; it has 3.3333+ times more notations. It emulates natural cellular growth and chemical bonding. Now, that was enough to get us going, yet we knew along the way we would find many other foundational reasons. Not too much later, we decided to start at the Planck length and just multiply by two. It worked out better and kind-of-sort-of confirmed our earlier work. That became our next version 2.0.0.1 which you see here. What does it mean and what can be done with the data? |
| 1. Our universe view initially had 202.34 to 205.11 steps. Using just the doublings of the Planck Units, there are between 201 and 202. Notwithstanding, this chart is a simple tool to help order information. When we began finding simple math errors within Version 1, we turned to the professionals. A leading astrophysicist said, “There are 205.11 notations.” Then on May 2, 2012, a retired NASA physicist, Joe Kolecki, made the calculation based on the results of the Baryon Oscillation Spectroscopic Survey (BOSS). He reported 202.34 notations. We trusted them both so we used that range. Then, in December 2014 we emerged with our own figure based simply on the doublings of the Planck Time and the 13.78 billion years, estimated age of the universe Yes, we found between 201 and 202 doublings.
2. The Planck Length, the first step and the next 60 steps. We have thought and thought about the Planck length. It is an elusive concept defined by three fundamental physical constants: the speed of light in a vacuum, Planck’s constant, and the gravitational constant. Yet, what is it? For over 100 years, people have attempted to define it more richly than 1.616×10−35 meters. Thought experiments anybody? Perhaps it is time to engage some of the students in some speculative thinking. I have asked among the most-curious of them, “What is the next step? Can we do a series of thought experiments?” The questions continued, “Could we just start by constructing simple models within the first ten steps and then become increasingly complex? Could this study be a pre-science or hypostatic science where we begin to see the interface between perfection and imperfection?” So where do we begin? First, of course, we will have to assume that Max Planck was right and his concept is a good place to begin. Second, even if the Planck Length is a dimensionful or a dimensionless number, it is still an actual measurement of a physical unit and it can be multiplied by 2. And third, it can be understood to be a very special case of a simple vertex, some might say a point. It is anybody’s guess if it defines some kind of special singularity. As a simple vertex, when multiplied by 2, there are two vertices. Freeman Dyson, physicist-exemplar with the Institute for Advanced Studies of Princeton, New Jersey argues that when we multiply by two, we should actually be multiplying by three, one for each dimension of space. I would counter that each vertex exists in three-dimensions but each is still a singular vertex. It doesn’t much matter anyway; there are plenty of vertices to go around. Within ten steps, multiplying by 2, there are 1024 vertices. Within twenty steps, there are over a million. Within 30 steps there are over a billion, in 40 steps over a trillion, in 50 steps over a quadrillion (1000-trillion), and at 60 over a quintillion (1,152,921,504,606,846,976). One could do very complex geometries with all those vertices. This all started with Plato’s five basic solids and thoughts about basic structure. Though most people do not give it much thought, it has been studied throughout much of our history, seemingly formalized by Pythagoras and extended by Plato. Our working concept was that the basic structure of the five platonic solids in some way permeates every subsequent layer (notation, doubling, layer or step). And, if this simple-yet-idiosyncratic worldview can hold water, then in a substantial way, these five figures would, in very special ways, become the backbone of our constants and universals. Attempting to Set This Work With Constants and Universals How do we go about defining what is truly universal and constant? Certainly not an easy task, most often based on a combination of logic, mathematics, and consistent measurements, the constants have proven true throughout all time and within any space. The universals are in part based on those constants as understood by the most-respected scholars throughout time and they have generalized and extended these constants in meaningful ways. Some people believe these concepts open pathways to understand how it is that there is space and time, and human life and consciousness. Today, what has been rigorously dependent on the study of physics and then the other sciences, has evolved to include religion, logic, ethics, value, and even business. With that as a most-complex chemistry, a key question to ask is, “What concepts are shared by all of these disciplines?” Then we ask, “What concepts are the most simple?” And also, “What concepts could have a face of perfection?” Those three questions opened the way to a very simple platform, a generalized model within which to work. It is emergent, internally-dependent form – function (the faces of perfection) and the imperfect quantum world: This work dates back to 1979 at MIT regarding first principles with 77 leading, living scholars from around the world but that work went nowhere until the encounter with the geometry kids of Steve Curtis’s classes at John Curtis Christian School in River Ridge, Louisiana. From family to Wikipedia and back again to the family It is difficult to know if a set of ideas is worth pursuing. The first challenge after that class was to do a literature search. We found all kinds of supportive information but nothing using base-2 exponential notation. The next step was to test the ideas with friends and family. It is embarrassing to be naïve and wrong at the same time, so some caution was exercised. By March 2012, we had no serious detractors, yet no deep confirmation that the Big Board was really useful. To push the judgment and to have a foundation for collaboration, we wrote it all up in the style of Wikipedia for Wikipedia. When the first draft went up in April, it quickly found several protesters who said, “This is original research. It needs scholarly review before we will trust its efficacy.” By the first week of May, it had been taken down. Though it had a very short run, it was good theater. I learned early that idiosyncratic ideas are not much tolerated within the academy. In my very early days of study, the chairman of the MIT physics department, Victor Weisskopf, helped me with an invitation to visit with John Bell at CERN Laboratories. Bell’s inequality equations as applied to the Einstein-Podolsky-Rosen thought experiment of 1935 had rendered most enigmatic experimental results. Though way over my head, I knew enough to ask a few questions. Yet, scholars demand informed questions, so, there were times I appeared naive. Always there was more to learn about the nature of information, the nature of thought, and the very nature of a thing. What is a photon? In what ways is it a carrier of electromagnetism? Although that was way back in1977, those domains of inquiry still swirl with questions. So now, with this rather skeletal model of the Big Board as our working construct, it was easy to wonder, “Have we come full circle? Are we back looking at the same questions that we were asking in throughout the ’70s, particularly in 1979?” So, to get properly oriented, based on that simple construct, order-continuity, relations-symmetry, and dynamics-harmony, are there particular questions that could be asked to clarify a path? For example, how is it that there is continuity between layers? What precipitates discontinuity? When is there symmetry-making and symmetry-breaking? What algorithms and formulas might make these simple interior models begin to cohere and function in such a way as to explain the phenomena within theoretical physics and quantum theory? To get perspective on it all, a group at the high school is focusing on it. The Argonne National Laboratory has sent us fifteen highly-exacting photographs from the work of their scientists within the small-scale world and the students have been challenged to take each photograph and assign it to a notation. Nikon’s Small World photographs from their annual calendar and contest are also being used. I have confirmed a comment by Prof. Dr. John Baez about this construct being idiosyncratic, and by asking questions of leading scholars around the world, have become the personification of idiosyncratic. From ideas, to theories, to constructs, to mathematics, I have often heard and read that the simple models are more elegant than the complex and that simplicity has a special elegance and beauty. So, here within this paragraph will be the links to discussions and meetings with people, from our finest scholars to our most fresh-and-open children, when and where we have used this construct to explore the meaning and value of life. The next steps: The first 60 notations, steps, doublings or layers. To date, the only possibilities for measurement of any of those first 60 can is within colliders like the Large Hadron Collider at CERN labs. These colliders begin their work at the 66th notation and it is anybody’s guess as to how many notations have been utilized and articulated. The results from the colliders render a lot of data, but very little about the interface between information and the deepest structure of physicality. So, if nothing else, the imposed structure of base-2 notation could provoke new insights. For example, because there is an assumed inherent correspondence between layers, perhaps there are also analogical constructions within known notations and with information theory itself. Highly-Speculative ideas that just might open a path for thought experiments Consider the work of the International Organization for Standardization (ISO) on the Open Systems Interconnection (OSI). They use seven abstraction layers to define the form and function of networking, a rigorous communications system. If all 202.34 layers of the universe in some way use an analogous construct, then as the first steps toward a thought experiment, we might simply force the OSI model over the first 60 layers as a starting point for rather free-associations and speculations. For example, perhaps 1-to-10 in some way perform like the physical layer, 10-to-20 like a data link layer, 20-to-30 like the network layer, 30-to-40 like the transport layer, 40-to-50 like a presentation layer, and 50-to-60 are like the beginnings of the application layer. It seems a bit silly to explore the OSI analogue, but within analogies are possibilities of making the strange familiar and the familiar strange. When the “thought experiment” door is opened, all kinds of wild and crazy notions just might begin to flow. Just to get a feel for the numbers, we documented the climb up the 202.34 steps and put all those numbers on the web. An old acquaintance from MIT (and one of the world’s more rigorous-yet-speculative thinkers in combinatorial mathematics), Ed Fredkin suggests that it is akin to numerology. Perhaps. But new ideas have to start somewhere. If we suspend our harshest judgments that close doors and open ourselves to a new insights, by walking around in the chaos-confusion-and-the-unknown, sometimes new ideas and thoughts begin to catch a trace of coherency, and then rigorous, coherent thinking can follow. If you look at the first column on the left of the Big Board, and go all the way down to the first 40 notations, you’ll notice there are over one trillion vertices at the 40th notation. In the left-most column at step 34 is the word, SPECULATIONS. Below it is “Quantum State Machine.” At this point in time, there are over 140,000 references in Google. Assuming that even .1% are of interest, there are 140 references to research and consider. The Modulus for transformation opens even more research to consider the question, “What is the transformation from one notation to the next?” Perhaps Theta-Fushian functions address the issue. How do cubic functions – cubicities — apply? With just a cluster of four vertices, the tetrahedron becomes possible. With five, two tetrahedrons. With seven vertices the five-tetrahedron cluster (pictured above) could emerge. Using Chrysler’s description of their logo, we call it a Pentastar. Perhaps within such simplicity and with its imperfect binding (there is up to a 1.5 degree gap between faces), here is the beginning of an energy wheel that acts and works like quantum fluctuations. That gap is extended within the icosahedron and Pentakis dodecahedron. And here, between these structures we could be a heartbeat away from opening a new foundational study within physics-chemistry-biology, epistemology-and-mathematics, and cosmology. There is so much more to consider and ponder. On a somewhat more whimsical note, I concluded back in January 2012, in defense of the pursuit of this study, the following:
Thank you. -Bruce Footnote. In discussing this construction of the universe with physicist John Baez (University of California – Riverside), he commented, “Well, it’s an idiosyncratic view of the universe.” I said, “That’s it.” It became the initial title for this emerging paper. Yet, to advance the concepts, we needed a more challenging, less self-effacing title. And until we are quite readily and intelligently challenged, the current title shall carry this project forward. Perhaps the universe is nested in ways that we cannot measure or discern with a physical instrument other than the mind. If you find it of some interest, let us know. Please share your thoughts. It appears that we all need to re-examine the simplest concepts and parameters more closely. Could Plato’s five basic solids in some way hold each progression together in a mathematical relation? Is it meaningful in any way? We would all enjoy hearing from you. Please drop us a note! – BEC |
Simple facts
These simple facts are for children and students, yet really for us all, just to keep opening conduits to natural creativity. When adults grasp these facts, a possible new synthesis for one’s genius may well open.
Editor’s Note: There are obvious facts – not just ideas – that could stimulate a child’s natural creativity simply because these facts exercise part of the brain that engages spatio-temporal relations in basic ways. These all seem to be “basic-basics” that do not have much currency within education today. – Bruce Camber
Perhaps engaging these questions is a little like listening to Beethoven before one learns how to speak. Adults might benefit by exercising one’s brain in ways that expand one’s commonsense logic structure. More…
Fact #1: A most-basic, three-dimensional object in space-and-time is the tetrahedron.
 We all should know the object very well. Some adults may be a little familiar with the object, but generally it has no particular importance. It should. It is the one of the most basic building block of the sciences. Children should play with tetrahedrons and octahedrons as well as other kinds of building blocks. Now here is a postulate; it is also one of the most basic building blocks of epistemology and heuristics.
We all should know the object very well. Some adults may be a little familiar with the object, but generally it has no particular importance. It should. It is the one of the most basic building block of the sciences. Children should play with tetrahedrons and octahedrons as well as other kinds of building blocks. Now here is a postulate; it is also one of the most basic building blocks of epistemology and heuristics.
This image comes from our Small Business School television series back in 1997 when we were trying to model “People, Products, and Processes” of business. Look at the tetrahedron just above. There are four tetrahedrons within each corner. The center face is one of the four exterior faces of an octahedron. The other four faces of the octahedron are interior.
Fact #2: Most adults cannot tell you what is perfectly enclosed within the tetrahedron.

This is not just a lack of insight into geometry, it is a lack of insight into the basic structures of biology, chemistry and physics. It all starts with the sphere; connect the center points of just four spheres and you have begun the simple process of making a tetrahedron.
From Wikipedia: An animation of close-packing lattice generation. This image file (right) is licensed under the Creative Commons Share-Alike 2.5 Generic license.
Fact #3: The octahedron is is magical. It is also a most basic three-dimensional object.
 From the octahedron we start seeing squares for the first time. Yes, the ubiquitous square is derivative. Now most scientists, logicians, and geometers cannot tell you what is perfectly enclosed within the octahedron.
From the octahedron we start seeing squares for the first time. Yes, the ubiquitous square is derivative. Now most scientists, logicians, and geometers cannot tell you what is perfectly enclosed within the octahedron.
That is a profound educational oversight.
Within each corner there is an octahedron. There are six corners. With each face is a tetrahedron. There are eight faces. The tape inside defines four hexagonal plates that share a common center point. Notice the tape comes in four different colors, red, white, blue, and yellow.
The internal structure of the octahedron is simple but opens the way to complexity quickly. By making it a practice to look inside basic structure, the mind gets exercised in very special ways. Quickly, this simplicity-that-is-complexity becomes metaphorical. The mind begins seeing similarities, analogies, and metaphors everywhere. The mind begins making the strange familiar and the familiar strange. By going inside the octahedron one learns basic order, then basic relations that become functions that move the mind further within the interior world.
Fact #4: The Big Board – little universe. 
Using base-2 exponential notation, take the smallest measurement, called the Planck length (PL), and multiply it by two. There are 101 steps (“doublings”) to reach the width of a human hair and 101+ additional steps to reach the edges of the observable universe. It begs the question, “Is this a meaningful way to organize data?” And, it inherently asks another question using the five platonic solids: “Is there a basic structural support created by nesting objects within all 202+ steps?” At the very least, it helps to organize data. In the smallest scale, there is conceptual richness. From step 1 to 65, the sum of the distances is equal to one-Planck-Length-less-than-the–diameter-of-a-proton, yet there are over 36 quintillion primary points to make every conceivable model, of any object or thing in existence. Now that opens up an interesting thought experiment. More…
Background Story: Big Board-little universe
Why you should say “Yes” when asked to do a favor…
Date: December 28, 2011 (with small updates, March 24, 2013 )
From: Bruce Camber
To: Friends and family
Subject: Big Board – little universe using base-2 exponential notation
Strange things can happen when invited to be a “guest lecturer” (essentially just an assistant for students) within five high school geometry classes and for the teacher who is part of the extended family.
Have you ever seen the entire universe mathematically related and notated on one chart? In studying the platonic solids and base-2 notation, it seemed to be an interesting task to do the simple base-2 math to create the picture on the far right of this page. That one was first printed at the Office Max in Harahan, Louisiana on December 17. It measured 24″ by 120″ but that was too big and awkward. Two smaller charts, 12″ by 60″ were created the next day, December 18, 2011 for the classroom discussions on December 19.
The ten foot board was cut about in half and the top section was put in the front of the class and the bottom section in the back. On the walls on the left and right were the two five foot charts. It seemed a bit enchanting.
There were five high school geometry classes that were challenged to see the universe using Plato’s five building blocks to visualize it all. We used base-2 exponential notation. It was clearly more granular than base-ten. One divides by 2 or multiplies by 2 instead of by 10. There is a huge history of work done within the orders of magnitude that we could readily use. At first, we used an imaginary tetrahedron that was 1 meter on its side. Our actual models were 2.5 inches. We divided that tetrahedron in half over and over again until we reached a measurement within the range of the Planck length, considered the smallest possible measurement. We then multiplied by two until that number was somewhere in the range of “the edges of the observable universe.” Where we expected thousands of steps in either direction, on our first pass we found as few as 105 notations (and as many as 118) going smaller and 91 going larger. We reduced it to a chart with a color wheel as the background, printed it up, and called it, Big Board – little universe (Version 2.0.0.1 displayed).
It all started with Plato’s five basic solids and thoughts about basic structure. Though most people do not give it much thought, it has been studied throughout time, probably starting with Pythagoras and picked up later by Plato.
For many of the students, this encounter was our second time to explore these five basic solids. The very first time together in March 2011, the students explored models using clear plastic tetrahedrons and octahedrons. Both are pictured in the right column under the headings “…simplest parts.” To go inside these models, essentially dividing them in half, requires a little finesse. Simply divide each edge in half and that point becomes a new vertex. With the tetrahedron there are six edges and within the octahedron there are eight edges. Connect all the new vertices and you have the simplest internal structure. Within the tetrahedron are four half-sized tetrahedra in each corner and an octahedron in the middle. Within the octahedron there are six half-sized octahedrons in each corner and a tetrahedron in each of the eight faces.
The students also made icosahedra out of 12 tetrahedrons. It was quite a lot of fun.
The second time with these kids would be more of a challenge. It would be the day just prior to their Christmas break.
The universe in 202.34 -to- 206 steps. When we began finding simple math errors, the number of notations increased from 206 to 215 (it became our fudge factor). Then a leading astrophysicist said, “There are 206 notations.” Then on May 2, 2012, a NASA physicist made the calculation based on the results of the Baryon Oscillation Spectroscopic Survey (BOSS). He reported 202.34 notations. Looking under scientific notation and orders of magnitude, we could only find bits and pieces of this work on the web.
An earlier history began with the study of perfected states in space time.
Sometime around 2002, at Princeton with geometer, John Conway, the discussion focused on the work of David Bohm, once a physicist from Birbeck College, University of London. “What is a point? What is a line? What is a plane vis-a-vis the triangle? What is a tetrahedron?” Bohm’s book, Fragmentation & Wholeness, raised key questions about the nature of structure and thought. It occurred to me that I did not know what was perfectly and most simply enclosed by the tetrahedron. What were its most simple number of internal parts? Of course, John Conway, was amused by my simplicity. We talked about the four tetrahedrons and the octahedron in the center.
I said, “We all should know these things as easily as we know 2 times 2. The kids should be playing with tetrahedrons and octahedrons, not just blocks.”
“What is most simply and perfectly enclosed within the octahedron?” There are six octahedrons in each corner and the eight tetrahedrons within each face. Known by many, it was not in our geometry textbook. Professor Conway asked, “Now, why are you so hung up on the octahedron?” Of course, I was at the beginning of this discovery process, talking to a person who had studied and developed conceptual richness throughout his lifetime. I was taking baby steps, and was still surprised and delighted to find so much within both objects. Also, at that time I had asked thousands of professionals — teachers, including geometry teachers, architects, biologists, and chemists — and no one knew the answer that John Conway so easily articulated. It was not long thereafter that we began discovering communities of people in virtually every academic discipline who easily knew that answer and were shaping new discussions about facets of geometry we never imagined existed.
Of course, I blamed myself for getting hung up on the two most simple structures… “You’re just too simple and easily get hung up on simple things.”
My family knows about this curious hang up of mine. They have seen these models on my desk. We made a pseudo-Rubik’s cube type of game out of the octahedron. One of younger ones in the family is the geometry teacher in the family’s small private high school. “Come in and introduce the kids to Plato’s five basic solids.” That’s about my level. In so many ways, those kids were actually more advanced than me.
During one of my days with them, we made icosahedrons with twenty tetrahedrons. I called it squishy geometry, but told them that I have yet to find a good discussion about it under quantum geometry or imperfect geometries, “…but when I find it, I’ll, report in.”
At first, our dodecahedron was a simple paper thing. We were trying to think of its simplest number of parts… “Could it be twelve odd objects coming into a center point, each with a pentagonal face and three triangular sides?” It didn’t seem like it would readily be extensible. On my desk was a “Chrysler logo” made using five tetrahedrons. There was always a gap — squishy geometry — but thought, “What would a pseudo-dodecahedron look like if it were made of twelve of those pentagonals (each made up of five tetrahedrons)?” Very quickly we had a model. A few hours later we were filling it with Play Doh to see what was within it. And just within, we found an icosahedron waiting.
Now that was fascinating to us, but, is it? Is it common knowledge among all the best-of-the-best within mathematics, chemistry, and physics? We are still not sure.
In thinking about a sequel class to that earlier time together, we began focusing on exponential notation. Having learned a little about Base 2 notation — my first time over these grounds — we put these pages up on this website to begin to share it with a wider audience: http://bblu.org
If you find it of some interest, there are links to more background pages from both.
Can Plato’s five most basic objects in some way hold each progression together in a mathematical relation? Is it meaningful in any way? We would all enjoy hearing from you.
Please drop us a note! – BEC